Table of Contents
Ejemplos de Función de Producción
Ejemplo 1: Función de Producción Cobb Douglas
La función de producción Cobb Douglas es un ejemplo de una función de producción con múltiples inputs (al menos 2) y que muestra un rendimiento marginal decreciente.
La Función de Producción Cobb Douglas tiene la siguiente forma:
Q(L,K) = A Lβ Kα
Donde:
L:trabajo
K:capital
Q:producción
A>0
0<α<1
0<β<1
Las principales características de la función de producción Cobb Douglas son:
- El producto marginal es positivo y decreciente
- La elasticidad de producción es constante
- Los retornos a escala son α+β
Ejemplo numérico:
A = 50
α = 0.7
β = 0.3
El gráfico de este ejemplo es:
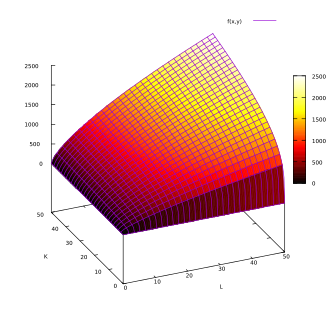
Ver también: Función de Producción Cobb-Douglas
Ejemplo de una función de producción linear
Esta función de producción es la mas simple. En este ejemplo, el producto tiene una relación directa con la cantidad utilizada de un solo factor de producción.
Por ejemplo, sin un robot puede producir 100 remeras por hora, y no existen otros factores de producción, la función de producción será:
Q = 100 K
Donde:
- Q = Cantidad de Remeras producidas por hora
- K = Cantidad de Robots empleados en la producción
El gráfico de este ejemplo es:
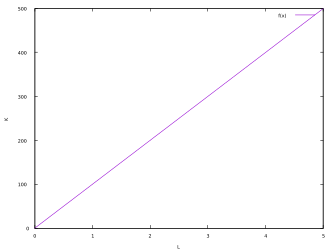
Ejemplo 3: Un solo factor de producción con retornos decrecientes
Este ejemplo es una extensión del ejemplo anterior, se trata de una función de producción con un solo input, pero a medida que aumenta su cantidad utilizada en la producción, la producción aumenta, pero en una cantidad cada vez menor.
Por ejemplo, si el primer robot produce 100 remeras, pero el segundo, en lugar de producir 100 adicionales produce 86; el tercero agrega 82. y así sucesivamente.
Un ejemplo numérico es el siguiente:
Q = 100 * K 0.9
El gráfico de la función de producción de este ejemplo es:
Como vemos, a medida que se agregan robots, la diferencia entre la cantidad producida por una función de producción linear y una función de producción con retornos decrecientes es mayor a medida que aumenta la cantidad utilizada del factor de producción.
Ejemplo 4: La función de producción CES
Esta función de producción tiene, como su nombre lo indica, una elasticidad de sustitución entre los factores de producción constante.
Un ejemplo de una función de producción CES es:
Q = F (a * Kα + (1 - a) L α)1/a
Ejemplo 5: Función de Producción de Proporciones Fijas
En un proceso productivo con factores de producción fijos, cada factor es necesitado en una relación fija con respecto al resto de los factores de producción. Por ejemplo, si se necesita una persona por computadora, y esta proporción es fija, cuando agregamos una persona adicional, sin agregar una computadora, la producción no varía. Lo mismo sucede si agregamos una computadora y no agregamos una persona.
En este ejemplo, la proporción (fija) es 1:1, pero esta proporción puede ser otra. Lo importante para este tipo de función de producción, es que la proporción sea fija.
Ejemplo de una función de producción de proporciones fija:
Q = min {L,K}
Ejemplo 6: Función de Producción de Sustitutos Perfectos
En la función de producción con factores sustitutos perfectos, un input puede ser sustituido por otro sin que se modifique el output.
Ejemplo:
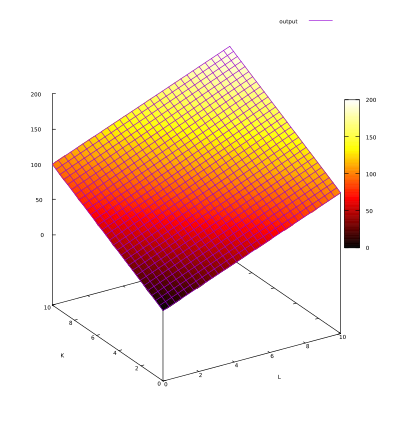
Q = aL + aK
Si aumenta L en 10 y al mismo tiempo disminuye K en 10, la cantidad producida no se modifica.
Discussion