Función de Producción Cobb-Douglas

La función de producción Cobb-Douglas es una forma particular de la Función de Producción.

La forma de la función de producción es la siguiente:

Q(L,K) = A L^βK^α

Donde:

• L:trabajo
• K:capital
• Q:producción
• A>0
• 0<α<1
• 0<β<1

Gráfico de una función de producción Cobb-Douglas:

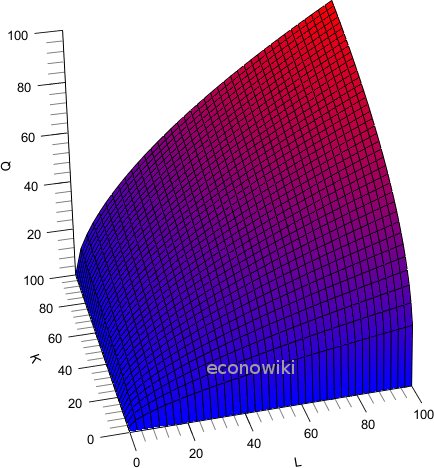
La función de producción Cobb-Douglas tienen ciertas características que la hacen muy útiles a la hora de construir modelos económicos que representan la producción

Algunas de las ventajas de la función de producción Cobb-Douglas son:

1. El producto marginal es positivo y decreciente.
2. La elasticidad de producción es constante e igual a α para K o β para L.
3. Los retornos a escala son α+β

Examinemos ahora estas características mas detenidamente:

Este comportamiento del producto marginal suele observarse en muchas funciones de producción de la vida real. Para obtener el producto marginal de un factor, derivamos el producto total respecto al factor de producción en cuestión; por ejemplo, si estamos analizando el producto marginal del capital:

∂Q / ∂K =

= α * (A L^β) K^(α-1)

Cabe recordar que α es positivo y menor que 1, por lo tanto, esta función será positiva y decreciente. Es positiva porque todos los elementos que la componen son positivos, entonces a medida que aumenta el capital, aumenta también la producción total. Es menor que uno, porque al ser α positivo y menor que 1, (α-1) es negativo, entonces al aumentar K aumenta la producción total, pero cada vez menos (si lo deseas, puedes calcular la derivada segunda, la cual es negativa).

Gráficamente:

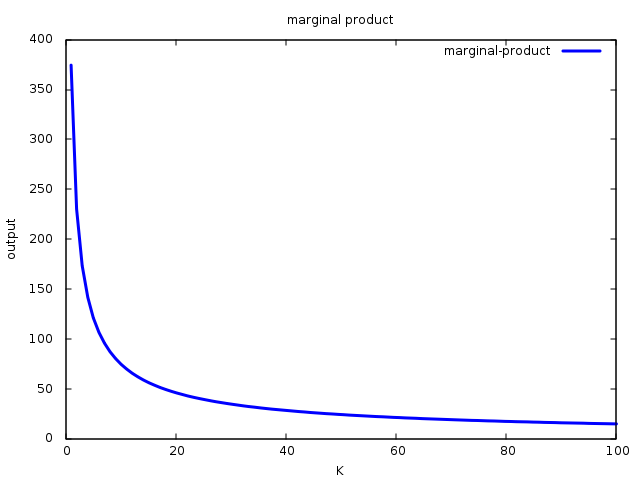
La elasticidad de producción se define como el cambio porcentual en la producción ante un cambio porcentual en alguno de los factores de producción.

En el caso de la función de producción Cobb-Douglas, la elasticidad de producción es constante. La elasticidad de producción del factor trabajo es β y la elasticidad de producción del factor capital es α.

A continuación, demostraremos porqué la elasticidad de producción es constante:

Por definición, la elasticidad de producción es:

(∂Q/Q) / (∂L/L) =

= (∂Q/∂L) / (Q/L) Es decir, el producto marginal del trabajo dividido el producto medio.

= [ Aβ L^β-1) K^α ] / [ A L^β K^α / L ]

Como 1/L es igual a L^-1, AL^βK^α/L se convierte en AL^β-1K^α, entonces, la elasticidad de producción es:

= AβL^β-1K^α / AL^β-1K^α

La única diferencia entre el numerador y el denominador es β, entonces:

Elasticidad de producción = AβL^β-1K^α / AL^β-1K^α = β

Los retornos a escala miden el cambio proporcional en la cantidad producida, ante un cambio proporcional en la cantidad utilizada de todos los factores de producción.

Si aumentamos todos los factores de producción en una constante c, el nuevo nivel de producción es:

Q^' = A(cL)^β(cK)^α

= Ac^βL^βc^αK^α

= c^βc^αAL^βK^α

= c^β+αQ

Entonces, si aumentamos la cantidad utilizada de todos los factores de producción en c, la producción aumentará en c^β+α.

Si β+α = 1, la producción también aumentará en c. En este caso, se dice que la función de producción tiene retornos constantes a escala.

Si β+α < 1, la proporción de aumento de la producción será menor que la proporción de aumento de los factores. En este caso, se dice que la función de producción tiene rendimientos decrecientes a escala.

Si β+α > 1, la proporción de aumento de la producción será mayor que la proporción de aumento de los factores. Es este caso, se dice que la función de producción tiene rendimientos crecientes a escala.

Elasticidad de Producción de una Función de Producción Cobb-Dogulas