Table of Contents
Exemplos de Funções de Produção
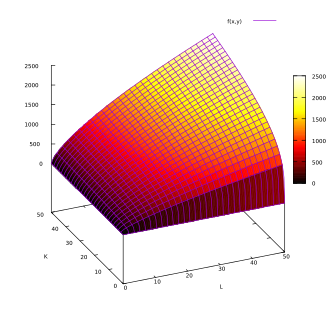
Exemplo 1: Função de Produção Cobb Douglas
A função de produção Cobb Douglas é um exemplo de uma função de produção com múltiplas fatores de produção (pelo menos 2) e que mostra um rendimento marginal decrescente.
A função de produção Cobb Douglas tem a seguinte forma:
Q(L,K) = A Lβ Kα
Onde:
L: trabalho
K: capital
Q: produção
A> 0
0 <α <1
0 <β <1
As principais características da função de produção Cobb Douglas são:
- O produto marginal é positivo e decrescente
- A elasticidade da produção é constante
- Os retornos de escala são α + β
Exemplo numérico:
A = 50
α = 0,7
β = 0,3
O gráfico neste exemplo é:
Veja também:
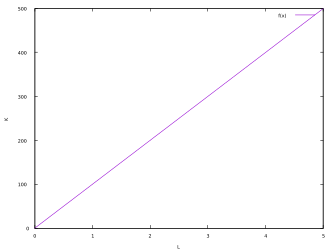
Exemplo de uma função de produção linear
Esta função de produção é a mais simples. Neste exemplo, o produto tem uma relação direta com a quantidade usada de um único fator de produção.
Por exemplo, sem um robô pode produzir 100 camisetas por hora, e não há outros fatores de produção, a função de produção será:
Q = 100 K
Onde:
- Q = Número de camisetas produzidas por hora
- K = número de robôs utilizados na produção
O gráfico neste exemplo é:
Exemplo 3: Um único fator de produção com retornos decrescentes
Este exemplo é uma extensão do exemplo anterior, é uma função de produção com uma única entrada, mas à medida que a quantidade utilizada na produção aumenta, a produção aumenta, mas em uma quantidade cada vez menor.
Por exemplo, se o primeiro robô produz 100 camisetas, mas o segundo, em vez de produzir um adicional de 100, produz 86; o terceiro adiciona 82, e assim por diante.
Um exemplo numérico é o seguinte:
Q = 100 * K0,9
O gráfico da função de produção neste exemplo é:
Como podemos ver, à medida que os robôs são adicionados, a diferença entre a quantidade produzida por uma função de produção linear e uma função de produção com retornos decrescentes é maior à medida que a quantidade usada do fator de produção aumenta.
Exemplo 4: A função de produção do CES
Esta função de produção tem, como o próprio nome indica, uma elasticidade de substituição entre os fatores de produção constante.
Um exemplo de uma função de produção do CES é:
Q = F (a * Kα + (1 - a) L α)1/a
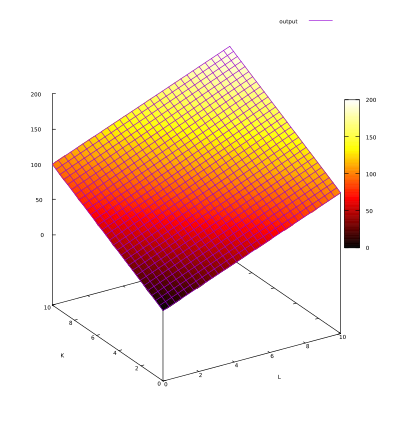
Exemplo 5: Função de Produção de Proporções Fixas
Em um processo de produção com fatores de produção fixos, cada fator é necessário em uma relação fixa com relação aos demais fatores de produção. Por exemplo, se uma pessoa é necessária por computador e essa proporção é fixa, quando adicionamos uma pessoa, sem adicionar um computador, a produção não varia. A mesma coisa acontece se adicionarmos um computador e não adicionarmos uma pessoa.
Neste exemplo, a proporção (fixa) é 1: 1, mas essa proporção pode ser diferente. O importante para esse tipo de função de produção é que a proporção é fixa.
Exemplo de uma função de produção de proporções fixas:
Q = min {L, K}
Exemplo 6: Função de Produção de Substitutos Perfeitos
Na função de produção com fatores substitutos perfeitos, um fator pode ser substituída por outro factor sem modificar a saída.
Exemplo:
Q = aL + aK
Se L aumenta em 10 e ao mesmo tempo K diminui em 10, a quantidade produzida não é modificada.
Discussion