Função de produção Cobb-Douglas
A função de produção Cobb-Douglas é uma forma particular da função de produção.
A forma da função de produção Cobb-Douglas é a seguinte:
Q(L,K) = A LβKα
Onde:
- L:trabajo
- K:capital
- Q:producción
- A>0
- 0<α<1
- 0<β<1
Gráfico de uma função de produção Cobb-Douglas:
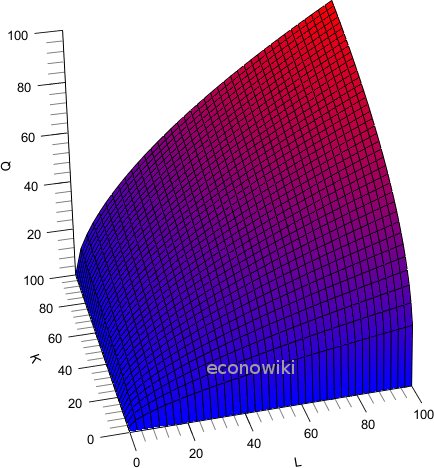
A função de produção Cobb-Douglas têm certas características que a tornam muito útil ao construir modelos econômicos que representam a produção.
Algumas das vantagens da função de produção Cobb-Douglas são:
O produto marginal é decrescente e positiva. Elasticidade de produção é constante e igual a K α ou β de L. Retornos de escala são α + β
O produto marginal é positivo e decrescente
Esse comportamento do produto marginal é visto em muitas funções de produção da vida real. Para obter o produto marginal de um fator, derivamos o produto total respeito do fator de produção em questão; por exemplo, se estamos analisando o produto marginal do capital:
∂Q / ∂K =
= α * (A Lβ) K(α-1)
Lembre-se que α é positivo e menor que 1, portanto, essa função será positivo e decrescente. É positivo porque todos os elementos que a compõem são positivos, então aumenta o capital, também aumenta a produção total. É menor que um, porque α é positivo e menor que 1, (1-α) é negativo, em seguida, aumentar o K aumenta a produção total, mas cada vez menos (a derivada de segunda ordem é negativa).
Graficamente:
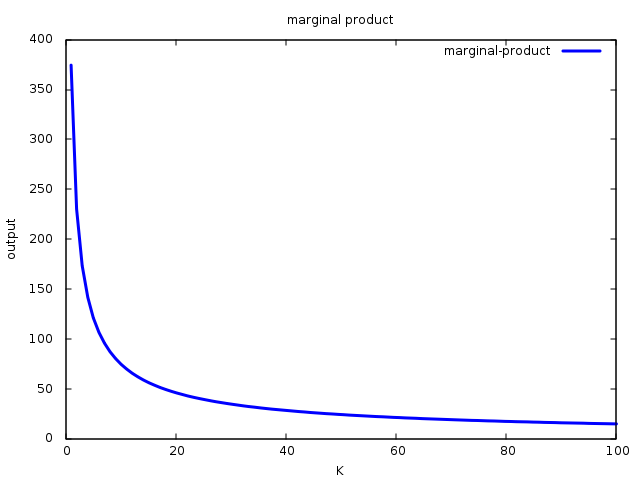
A elasticidade de produção é constante
A elasticidade de produção é definida como a variação percentual na produção quando lá uma variação percentual em algum dos fatores de produção.
No caso da função de produção Cobb-Douglas, a elasticidade de produção é constante. A elasticidade da produção do factor trabalho é β e a elasticidade da produção do capital é α.
Vamos mostrar por que a elasticidade da produção é constante:
Por definição, a elasticidade da produção é:
(∂Q/Q) / (∂L/L) =
= (∂Q/∂L) / (Q/L) Isto é o produto marginal do trabalho dividiu o produto médio.
= [ Aβ Lβ-1) Kα ] / [ A Lβ Kα / L ]
1/L é igual a L-1, ALβKα/L se converte em ALβ-1Kα, em seguida, a elasticidade de produção é:
= AβLβ-1Kα / ALβ-1Kα
A única diferença entre o numerador eo denominador é β, então:
Elasticidade de produção = AβLβ-1Kα / ALβ-1Kα = β
Retornos de escala são α + β
Os retornos de escala medem o variação proporcional na quantidade produzida, até uma alteração proporcional na quantidade utilizada de todos os factores de produção.
Se aumentamos todos os fatores de produção em uma constante c, o novo nível de produção é:
Q' = A(cL)β(cK)α
= AcβLβcαKα
= cβcαALβKα
= cβ+αQ
Então, se aumentarmos a quantidade utilizada de todos os factores de produção em c, a produção aumentará em c β + α.
Se β + α = 1, a produção também aumentará em c. Neste caso, diz-se que a função de produção tem retornos constantes de escala.
Se β + α < 1, a proporção de aumento da produção será inferior a proporção dos fatores de aumento. Neste caso, diz-se que a função de produção tem retornos decrescentes de escala.
Se β + α > 1, a proporção do aumento de produção será maior do que a proporção dos fatores de aumento. Neste caso, diz-se que a função de produção tem retornos crescentes à escala.
Discussion